advertisingbion.blogg.se - Base of isosceles triangle calculator

#Base of isosceles triangle calculator how to#

The properties of some triangles, like right triangles, are usually interesting and shocking, even for non-mathematicians. Geometry and polygons, especially triangles, always come together. You can, of course, be even more efficient and just use our calculator. Still, with a bit of skill, you can use the same idea and calculate the area of a parallelogram using right-angled triangles. For other parallelograms, the process becomes a bit more complicated (it might involve up to 4 right triangles of different sizes). It was a simple example of a rectangle, but the same applies to the area of a square. This is precisely what we already saw by just cutting the rectangle by the diagonal. If we think about the equations, it makes sense since the area of a rectangle of sides a and b is exactly area = a × b, while for the right triangle is area = base × height / 2 which, in this case, would mean area = a × b /2.

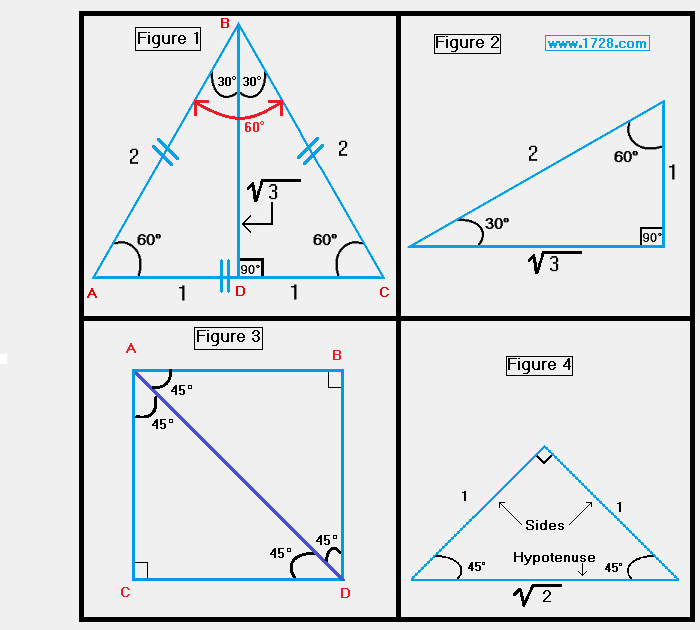
This means that the area of the rectangle is double that of each triangle. Looking at the triangles, there is no need to use the right triangle calculator to see that both are equal, so their areas will be the same. If we separate the rectangle by the diagonal, we will obtain two right-angled triangles. Now draw a trace on one of the diagonals of this rectangle. Assuming that the shorter side is of length a, the triangle follows: The consequences of this can be seen and understood with the 30 60 90 triangle calculator, but for those who are too lazy to click the link, we will summarize some of them here. These angles are special because of the values of their trigonometric functions (cosine, sine, tangent, etc.).

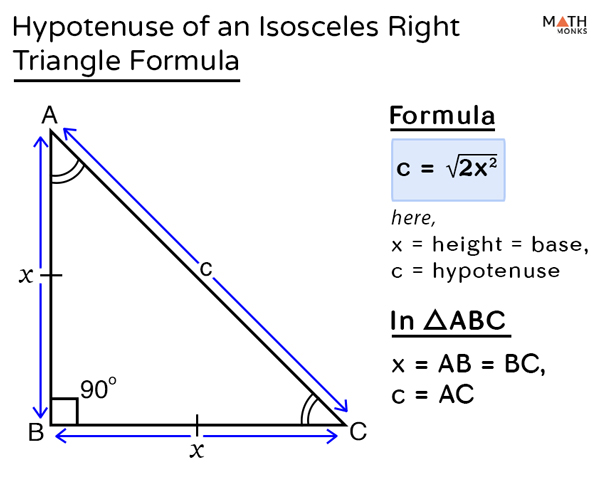
The name comes from having one right angle (90°), then one angle of 30°, and another of 60°. For those interested in knowing more about the most special of the special right triangles, we recommend checking out the 45 45 90 triangle calculator made for this purpose.Īnother fascinating triangle from the group of special right triangles is the so-called "30 60 90" triangle. That is why both catheti (sides of the square) are of equal length. This right triangle is the kind of triangle that you can obtain when you divide a square by its diagonal.

You have to use trigonometric functions to solve for these missing pieces.

#Base of isosceles triangle calculator how to#

In such cases, the right triangle calculator, hypotenuse calculator, and method on how to find the area of a right triangle won't help. Sometimes you may encounter a problem where two or even three side lengths are missing.

If an angle is in degrees – multiply by π/180.

If an angle is in radians – multiply by 180/π and.

There is an easy way to convert angles from radians to degrees and degrees to radians with the use of the angle conversion: An easy way to determine if the triangle is right, and you just know the coordinates, is to see if the slopes of any two lines multiply to equal -1. So if the coordinates are (1,-6) and (4,8), the slope of the segment is (8 + 6)/(4 - 1) = 14/3. The sides of a triangle have a certain gradient or slope. Now we're gonna see other things that can be calculated from a right triangle using some of the tools available at Omni.

As a bonus, you will get the value of the area for such a triangle.

Insert the value of a and b into the calculator and.

Now let's see what the process would be using one of Omni's calculators, for example, the right triangle calculator on this web page:

The resulting value is the value of the hypotenuse c.

Since we are dealing with length, disregard the negative one.

The square root will yield positive and negative results.

Let's now solve a practical example of what it would take to calculate the hypotenuse of a right triangle without using any calculators available at Omni: A Pythagorean theorem calculator is also an excellent tool for calculating the hypotenuse. We can consider this extension of the Pythagorean theorem as a "hypotenuse formula". To solve for c, take the square root of both sides to get c = √(b²+a²). In a right triangle with cathetus a and b and with hypotenuse c, Pythagoras' theorem states that: a² + b² = c². The hypotenuse is opposite the right angle and can be solved by using the Pythagorean theorem. However, we would also recommend using the dedicated tool we have developed at Omni Calculators: the hypotenuse calculator. If all you want to calculate is the hypotenuse of a right triangle, this page and its right triangle calculator will work just fine.